What Is The Effect Of Shifting An Unsigned Number In A Register 1 Bit To The Right
Logical Vs. Arithmetic Shift
Logical Shift and Arithmetics Shift are scrap manipulation operations (bitwise operations).
Logical Shift
- A Left Logical Shift of one position moves each scrap to the left by ane. The vacant least significant bit (LSB) is filled with nada and the most meaning fleck (MSB) is discarded.
- A Right Logical Shift of one position moves each scrap to the right by one. The least significant bit is discarded and the vacant MSB is filled with zero.
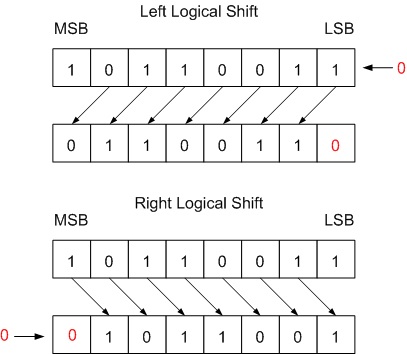
Fig. 1 Logical Shift past one bit
Arithmetic Shift
- A Left Arithmetic Shift of i position moves each fleck to the left past 1. The vacant least significant bit (LSB) is filled with zero and the most meaning bit (MSB) is discarded. It is identical to Left Logical Shift.
- A Correct Arithmetic Shift of 1 position moves each bit to the right by one. The least significant fleck is discarded and the vacant MSB is filled with the value of the previous (now shifted one position to the right) MSB.
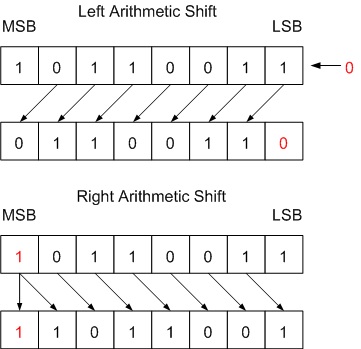
Fig. one Left and Correct Arithmetic Shift by One Scrap
Arithmetics Shift operations tin can be used for dividing or multiplying an integer variable.
Multiplication past left shift:
The result of a Left Shift operation is a multiplication past 2north , where n is the number of shifted bit positions.
Instance:
Allow'due south accept the decimal number two represented as 4 chip binary number 0010. By shifting in to the left with one position we get 0100 which is 4 in decimal representation. If we shift information technology once again we get binary value 1000 which is 8 in decimal representation.
For unsigned representation, when the first "1" is shifted out of the left edge, the operation has overflowed. The effect of the multiplication is larger than the largest possible.
Shifting left on signed values as well works, but overflow occurs when the most significant bit changes values (from 0 to i, or 1 to 0).
Division by correct shift:
The result of a Right Shift performance is a partition by twon , where northward is the number of shifted scrap positions.
Example:
If we have the binary number 01110101 (117 decimal) and we perform arithmetic right shift past ane chip we get the binary number 00111010 (58 decimal). So we have divided the original number by 2.
If we accept the binary number 1010 (-six decimal) and we perform arithmetic correct shift by ane bit we become the binary number 1101 (-3 decimal). And then we accept divided the original negative number by 2.
Notation: The examples higher up apply two's complement representation.
Was this article helpful?
Share This Story, Choose Your Platform!
Source: https://open4tech.com/logical-vs-arithmetic-shift/
Posted by: millermandist37.blogspot.com


0 Response to "What Is The Effect Of Shifting An Unsigned Number In A Register 1 Bit To The Right"
Post a Comment